The Doob-h transform: a random walk conditionned to avoid obstacles
Let \(\mathcal X\) be finite and consider a Markov Chain \((X_t)_{t=0}^\infty\) on \(\mathcal X\) with transition matrix \(P(\cdot,\cdot)\).
Let \(A,B\subset \mathcal X\) be disjoint subsets of \(\mathcal X\) such that \(P(x,x)=1\) for \(x\in A\cup B\) and \(P(x,x)<1\) for \(x\notin A\cup B\). The elements of \(A\cup B\) are the only absorbing sites. We assume that for any \(x\in \mathcal X\setminus (A\cup B)\), there exists \(y\in A\) such that \(y\) is accessible from \(x\) (i.e., there exists a path from \(x\) to \(y\) with positive probability with respect to \(P(\cdot,\cdot)\)).
The Doob-h transform
Let \(h:\mathcal X\to[0,+\infty)\) be a harmonic and positive on \(\mathcal X\setminus (A\cup B)\). Define a matrix \(\check P\) by \[\begin{equation} \check P(x,y) = P(x,y) h(y) / h(x) \end{equation}\] for \(x\in \mathcal X\setminus (A\cup B)\) and \(y\in \mathcal X\), as well as \[\check P(x,x)=1\] for \(x\in A\cup B\).
This matrix \(\hat P(\cdot,\cdot)\) is again a transition matrix (check!) and called the Doob-h transform. For further expositions and references, see (Levin and Peres 2017).
Boundary conditions
Now, set \[h(x) = \mathbf P_x(\tau_A < \tau_B)\] where \(\tau_A = \min \{t\ge0: X_t\in A\}\) and \(\tau_B = \min \{t\ge0: X_t\in B\}\). In other words, \(h(x)\) is the probability, starting from \(x\), to hit \(A\) before hitting \(B\). Then \(h\) is positive on \(\mathcal X\setminus (A\cup B)\) (check!), and furthermore, for \(x\notin A\cup B\) \[\begin{equation} \check P(x,y) = \mathbf P_x [ X_1 = y | \tau_A < \tau_B]. \end{equation}\] Finally, \(h(x) = \mathbf P_x(\tau_A < \tau_B)\) satisfies both
- \(h(x) = 1\) for \(x\in A\) and \(h(z) = 0\) for \(z\in B\);
- \(h\) is harmonic at \(x\) for every \(x\notin A\cup B\);
and \(h(\cdot)\) is the unique solution of the linear system of equations given by 1 and 2 above. The equations in 1 are sometimes referred to as the boundary conditions.
A random walk conditioned conditioned to avoid obstacles
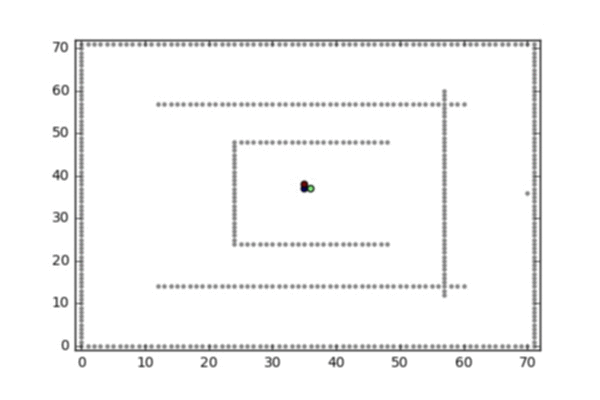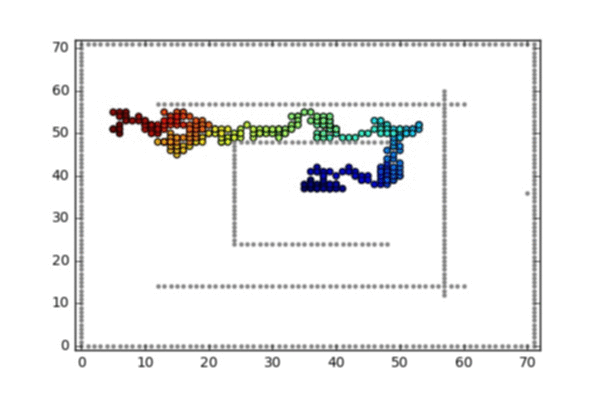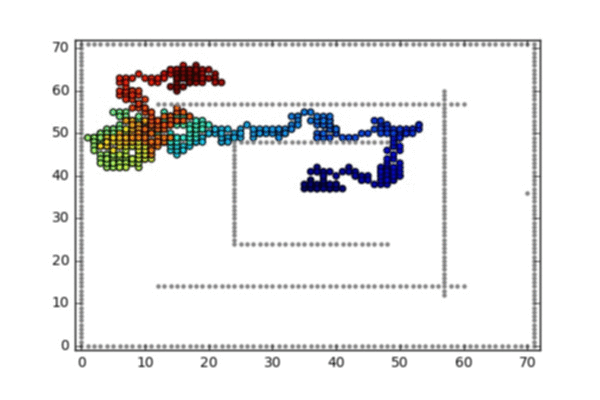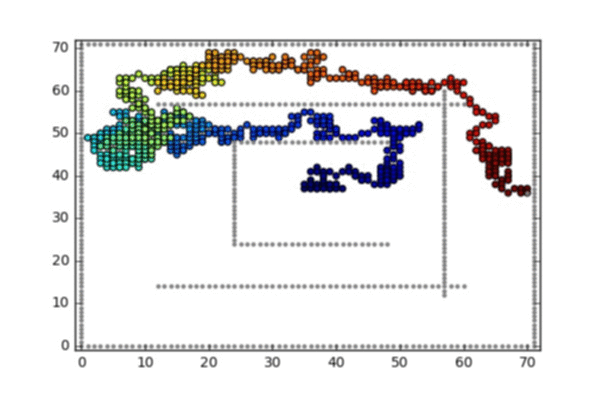
Starting from the transition matrix \(P(\cdot,\cdot)\) of a random walk in \(\mathbb Z\times \mathbb Z\), and given two subsets \(A\) (the targets) and \(B\) (repulsive walls), implementing the Doob-h transform \(\hat P(\cdot,\cdot)\) is easily implementable by solving the corresponding linear system that characterizes the function \(h\).
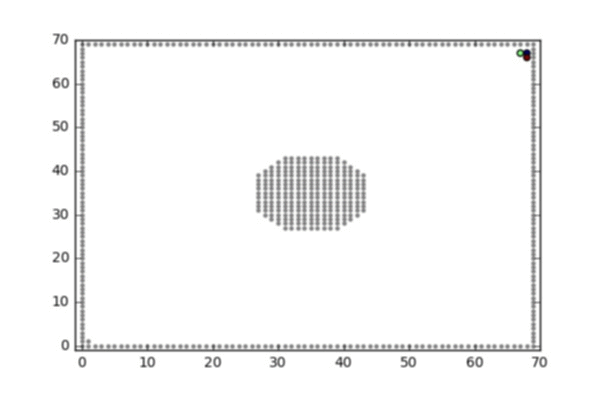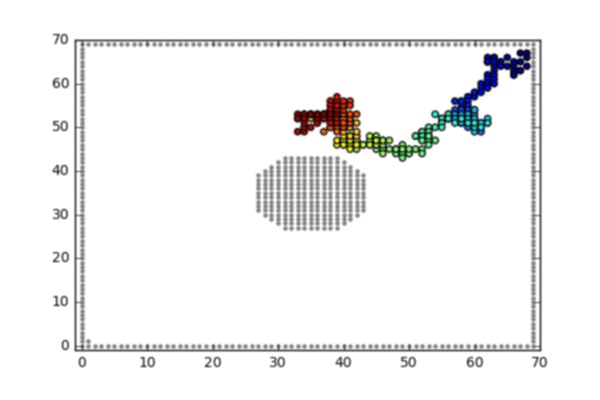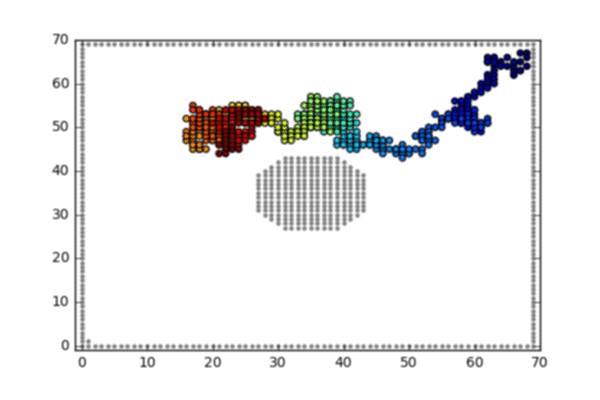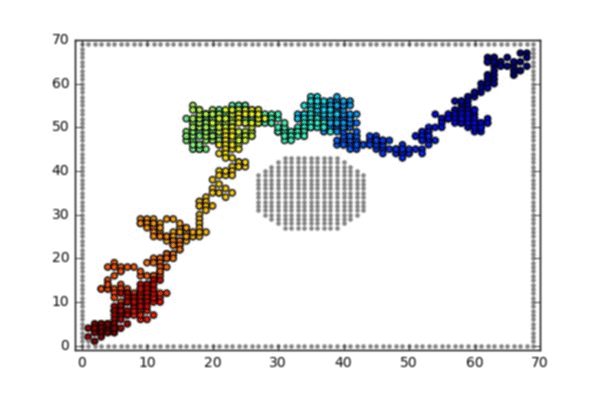
Two such conditoined random walks are illustrated below:
Illustrated animation 1

Illustrated animation 2